ЛОГАРИФМ ЧИСЛА. ОСНОВНАЯ ЛОГАРИФМИЧЕСКАЯ ТОЖДЕСТВО. ДЕСЯТЕЧНЫЙ ЛОГАРИФМ. НАТУРАЛЬНЫЙ ЛОГАРИФМ
Рассмотрим, как решать показательные уравнения:
\(3^{x}=81\) (1)
Запишем заданное уравнение так: \(3^x=3^4\), откуда \(x=4\)
В уравнении (1) неизвестен показатель степени.
Для решения уравнения использован способ, где левую и правую части уравнения нужно представить в виде степени с одинаковым основанием \(3\).
Рассмотрим уравнение \(2^x = 8\) (2). Размышляя так же, находим корень уравнения: \(x=3\). Попробуем решить уравнение \(2^x = 6\). Геометрическая иллюстрация представлена на рисунке.
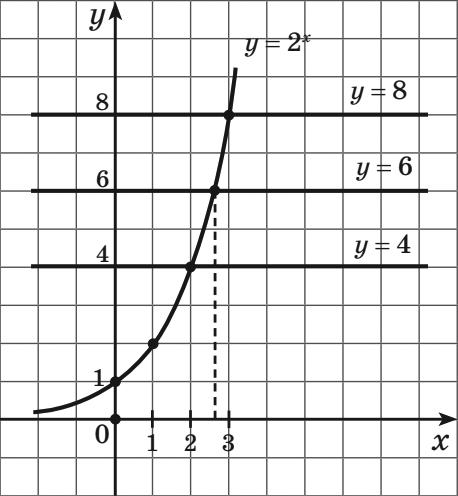
Понятно, что уравнение имеет один корень, но, в отличие от предыдущих случаев, где корни уравнения было не трудно найти (к тому же их можно найти и не пользуясь графиками), с уравнением \(2^x = 6\) у нас возникают определенные трудности: по графику мы не можем определить значение корня, а можем лишь установить, что этот корень находится на промежутке от \(2\) до \(3\).
Аналогично можно рассматривать и уравнение \(3^x = 5\), и уравнение \(10^x = 0,3\), и уравнение \(\left(\frac{1}{3}\right)^{x}=4\), и вообще любое уравнение вида \(a^x = b\), где \(a\) и \(b\) — положительные числа, \(a ≠ 1\). Единственный корень уравнения \(a^x = b\) записывают так: \(x=\log_{a}{b}\) (читают: «логарифм числа \(b\) с основанием \(a\)»).
Логарифмом положительного числа \(b\) с основанием \(a\), где \(a > 0\), \(a ≠ 1\), является показатель степени \(x\), к которому нужно поднести число \(a \), чтобы получить число \(b\).
Широко используют десятичные логарифмы — логарифмы с основанием \(10\). Десятичный логарифм числа \(b\) обозначают \(\lg{b}\) (без указания основания).
Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основой которых является \(e\): \(\ln{b}\) .
Такие логарифмы называют натуральными.
Натуральным логарифмом числа называют логарифм этого числа с основанием \(e\), где \(e\) — иррациональное число, примерно равное \(2,7\). Записывают \(\ln{b}\).
ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВ
При осуществлении преобразований выражений, содержащих логарифмы, выполнении вычислений и уравнений часто применяют различные свойства логарифмов. Рассмотрим основные из них.
Пусть \(a > 0, a ≠ 1, b > 0, c > 0, k\) — любое число (\(k ≠ 0)\). Тогда истинны формулы:
\(\log_{a}{bc}=\log_{a}{b}+\log_{a}{c}\) (1)
\(\log_{a}{\frac{b}{c}}=\log_{a}{b}-\log_{a}{c}\) (2)
\(\log_{a}{b^{k}}=k\log_{a}{b}\)
\(\log_{a^{k}}{b}=\frac{1}{k}\log_{a}{b}\) (3)
По основному логарифмическому тождеству
\(a^{\log_{a}{b}}=b\) (4)
\(a^{\log_{a}{c}}=c\) (5)
1) Умножив равенства (4) и (5), получим \(a^{\log_{a}{b}+\log_{a}{c}}=bc\), откуда по определению логарифма \(\log_{ a}{b}+\log_{a}{c}=\log_{a}{(bc)}\). Формула (1) доказана.
\(\log_{a}{(bc)}=\log_{a}{b}+\log_{a}{c}\)
Следствие 1. Если числа \(b\) и \(c\) одного знака, то имеет место равенство
\(\log_{a}{(bc)}=\log_{a}{|b|}+\log_{a}{|c∣}\)
2) Разделив равенства (4) и (5), получим \(a^{\log_{a}{b}-\log_{a}{c}}=\frac{b}{c}\), откуда за oпределением логарифма следует формула (2).
\(\log_{a}{\frac{b}{c}}=\log_{a}{b}-\log_{a}{c}\)
3) Если поднять основное логарифмическое тождество \(a^{\log_{a}{b}}=b\) к степени с показателем \(k\), получим \(a^{k\log_{a}{b}}=b^{k}\), откуда по определению логарифма следует формула (3).
\(\log_{a}{b^{k}}=klog_{a}{b}\).
Следствие 2. При любом целом \(k\) и \(b ≠ 0\) имеет место равенство
\(\log_{a}{b^{2k}}=2klog_{a}{|b|}\).
На практике применяют также свойства: \(\log_{a}{1}=0, \log_{a}{a} =1\).
Основные свойства логарифмов широко используют при преобразовании выражений, содержащих логарифмы. Отдельным видом таких преобразований является логарифмирование выражений.
Действие нахождения логарифма числа называют логарифмированием. Действие нахождения числа по его логарифму называют потенцированием.
Прологарифмировать одночлен означает выразить его логарифм через входящие в их состав логарифмы положительных чисел (обозначенных цифрами и буквами).
Применяя теоремы о логаримфее произведения, доли, степени и корня, можно прологарифмировать любое выражение, являющееся одночленом.
