Теорема косинусов
9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем записаться на уроки в Tutor-Math. В этой статье вы найдете самое важное про теорему косинусов.
Формулировка теоремы.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
\[a^{2}=b^{2}+c^{2}-bc \cos\alpha\]
Заметим, что теорема Пифагора является частным случаем теоремы косинусов для прямоугольного треугольника, поэтому иногда ее называют обобщенной теоремой Пифагора.
Следовательно, в произвольном треугольнике \(АВС\) выполняются равенства:
\(c^ 2 =a^ 2+ b^ 2-2abcosC\);
\(b^ 2 =a^ 2+ c^ 2-2accosB\);
\(a^ 2 =b^ 2+ c^ 2-2bccosA\).
С помощью теоремы косинусов можно, например, найти неизвестную сторону треугольника, если известно две другие стороны и один из углов.
Например, косинус угла \(С\) можно найти по формуле, выразив \(cosС\) из формулы теоремы косинусов:
\(cosC=\frac{a^ 2+ b^ 2-c^ 2}{2ab}\).
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-уроки по математике для детей и подростков.
Следовательно, теорема косинусов помогает решать треугольники.
Теорема косинусов удобна и для определения вида треугольника. Чтобы установить остроугольный, прямоугольный или тупоугольный треугольник достаточно найти знак косинуса его наибольшего угла. Из формулы косинуса угла ясно, что знак косинуса угла зависит от знака числителя дроби, поскольку знаменатель всегда положительный. Поэтому знак выражения \(a^2+b^2-c^2\) позволяет определить знак косинуса угла треугольника, а следовательно, и вид этого угла (острый, прямой или тупой).
Если \(c\) – наибольшая сторона треугольника и
\(a^2+b^2-c^2>0\), то угол \(C\) – острый, а треугольник – остроугольный;
\(a^2+b^2-c^2=0\), то угол \(C\) – прямой, а треугольник – прямоугольный;
\(a^2+b^2-c^2<0\), то угол \(C\) – тупой, а треугольник – тупоугольный.
Также с помощью теоремы косинусов можно доказать формулу медианы треугольника:
\(m_{a}= \frac{1}{2}\sqrt{2b^2+2c^2-a^2}\).
Решим несколько типовых задач по этой теме.
Задача 1. Найдите неизвестную сторону треугольника \(АВС\), если \(AB=5\) см, \(BC=8\) см, \( \angle B= 60^{\circ}\).
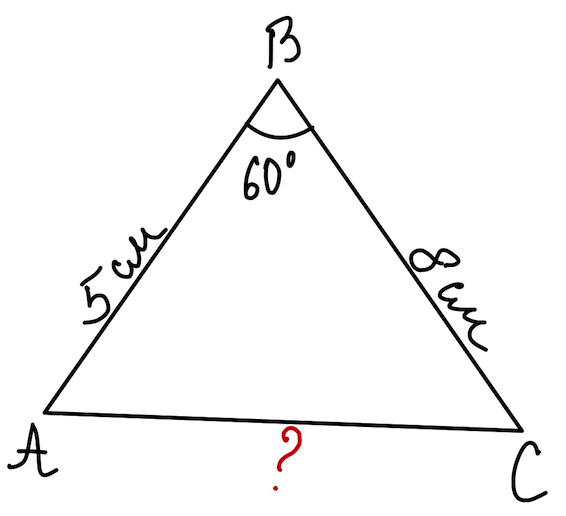
Дано: \(\triangle ABC\) , \(AB=5\) см, \(BC=8\) см, \( \angle B= 60^{\circ}\).
Найти: \(AC\).
Решение:
По теореме косинусов:
\(AC^ 2=AB^ 2+BC^ 2-2\cdot AB\cdot BC\cdot cosB\).
Подставляем данные из условия в формулу и получаем:
\(AC^ 2=5^ 2+8^ 2-2\cdot 5\cdot 8\cdot cos 60^{\circ}=25+64-2\cdot 5\cdot 8\cdot \frac{1}{ 2}=49\),
\(AC=7\) см
Ответ: \(AC=7\) см.
Задача 2. Докажите, что треугольник со сторонами \(8\) см, \(15\) см и \(17\) см прямоугольным.
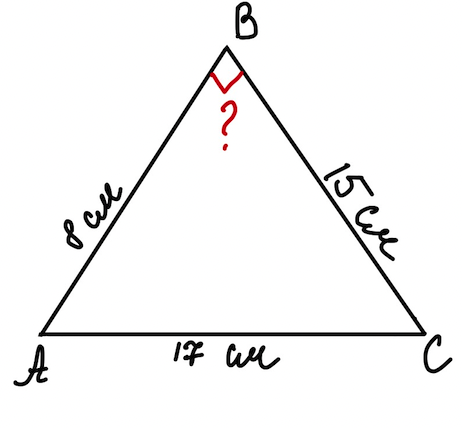
Дано: \(\triangle ABC\), \(AB=8\) см, \(BC=15\) см и \(AC=17\) см.
Доказать: \(\triangle ABC\) - прямоугольный.
Доказательство:
\(AC\) - самая большая сторона \(\triangle ABC\). Сравним с \(0\) значение выражения \(AB^ 2+BC^ 2-AC^ 2\). Подставляем данные из условия \(8^2+15^2-17^2=64+225-289=0\), следовательно \(\angle A\) - прямой, а \(\triangle ABC\) - прямоугольный.
Задача 3. Две стороны треугольника равны \(7\) см и \(8\) см, а угол против меньшей из них \(60^{\circ}\). Найдите третью сторону треугольника.
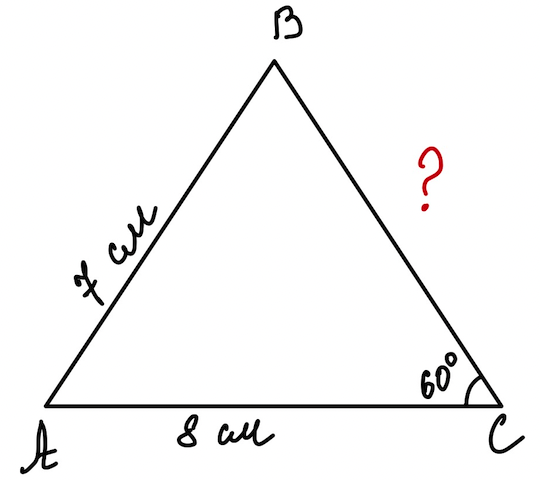
Дано: \(\triangle ABC\), \(AB=7\) см, \(AC=8\) см, \( \angle C=60^{\circ}\).
Найти: \(BC\).
Решение:
Пусть, сторона \(\triangle ABC\) \(BC=x\), тогда по теореме косинусов имеем: \(AB^ 2=BC^ 2+AC^ 2-2\cdot BC\cdot AC\cdot cosC\) .
Подставим значение из условия задачи, получим \(7^ 2=x^ 2+8^ 2-2\cdot 8\cdot x\cdot \frac{1}{2}\);
\(49=x^2+64-8x\);
\(x^ 2-8x+15=0\)
Решаем квадратное уравнение. Как решать квадратные уравнения описаны в этой статье.
\(D=64-60\), \(\sqrt{D}=2\)
\(x_1=5, x_2=3\)
\(BC=5\) см, или \(3\) см.
Ответ: \(3\) см или \(5\) см.
Задача 4. В равнобедренном треугольнике основание равно \(8\) см, а угол при основании - \(45^{\circ}\). Найдите боковую сторону треугольника.
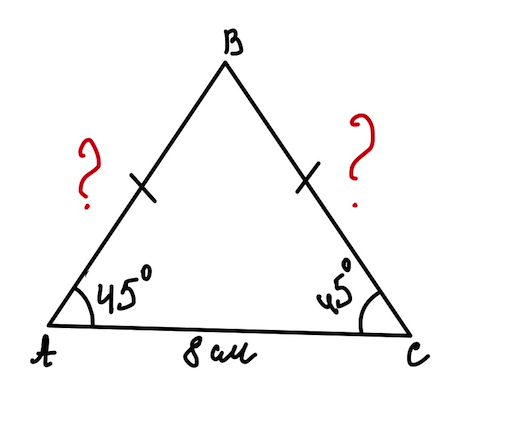
Дано: \(\triangle ABC\), \(AB=BC\), \(AC=8\) см, \( \angle A=45^{\circ}\).
Найти: \(AB\).
Решение:
Поскольку \(\triangle ABC\) - равнобедренный, \(AB=BC\), \( \angle A= \angle C=45^{\circ}\). Найдем \(\angle B\). По теореме о сумме китов в треугольнике \( \angle B=180^{\circ}-\angle A- \angle C=180^{\circ}-45^{\circ}-45^{\circ}=90 ^{\circ}\). Пусть (AB=BC=x).
По теореме косинусов:
\(AC^ 2=AB^ 2+BC^ 2-2\cdot AB\cdot BC\cdot cosB\);
\(64=x^ 2+x^ 2\);
\(2x^ 2=64\);
\(x^ 2=32\);
\(x=4\sqrt{2}\).
\(AB=BC=4\sqrt{2}\) см.
Ответ: \(4\sqrt{2}\) см.
Задача 5. Найдите косинус наибольшего угла треугольника, стороны которого равны \(5\) см, \(6\) см и \(9\) см.
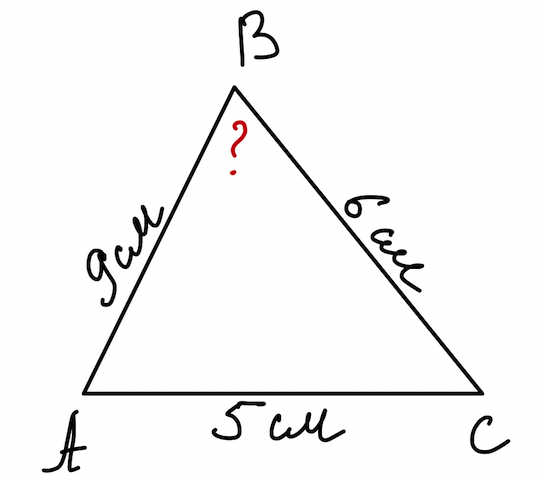
Дано: \(AB=9\) см, \(BC=6\) см, \(AC=5\) см.
Найти: \(cos\angle B\).
Решение:
Наибольший угол лежит напротив самой большой стороны. По теореме косинусов: \(cos\angle B=\frac{BC^ 2+ AC^ 2-AB^ 2}{2BC\cdot AC}=\frac{6^ 2+ 5^ 2-9^ 2}{2 \cdot 6\cdot 5}=\frac{-20}{12\cdot 5}=-\frac{1}{3}\).
Ответ: \(cos\angle B=-\frac{1}{3}\).
Остались вопросы? Ждем вас на наших уроках и мы с радостью дадим ответы на все вопросы по выбранному предмету.
