Натуральні числа

Натуральні числа. Цифри. Число нуль. Десятковий запис натурального числа

Тисячі років тому перед людьми вже виникала потреба рахувати, наприклад, членів родини, худобу, здобич, рибу тощо. Уміння рахувати й обчислювати потрібні і зараз, і навряд втратять свою актуальність найблищим часом.

Натуральні числа

Числа \(1, 2, 3, 4, 5, ...\), які використовують для лічби предметів, називають натуральними числами. Натуральні числа використовують також і для визначення порядку розміщення предметів. 

Цифри

Будь-яке натуральне число можна записати за допомогою десяти цифр: \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9\). Такий запис називають десятковим, а цифри — арабськими. Якщо натуральне число записане однією цифрою, то його називають одноцифровим, двома цифрами — двоцифровим і т. д.

Щоб простіше було читати натуральні числа, їх розби вають на групи справа наліво, по три цифри в кожній групі. Найперша група ліворуч може містити менше ніж три цифри. Наприклад: \(57 403\). Кожна група утворює класи: одиниць, тисяч, мільйонів і т. д. Кожен клас має три розряди: одиниць, десятків, сотень.

Число нуль

Якщо в числі відсутній якийсь розряд, то в запису числа на його місці стоїть цифра \(0\). Її також використовують для запису числа «нуль», яке означає «жодного».

Нуль не є натуральним числом

Натуральний ряд чисел

Усі натуральні числа, записані в ряд так, що за кожним числом іде наступне: \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...\) утворюють натуральний ряд чисел.

Властивості натурального ряду чисел:

• Має найменше число \(1\).
• Кожне наступне число більше за попереднє на \(1\).
• Не має найбільшого числа.

Хоч би яке велике число ми назвали, додавши до нього \(1\), отримаємо ще більше число

Римські цифри

Давні римляни користувалися іншими цифрами, які називають римськими. Їх використовують для запису чисел і нині, наприклад, для циферблата на годиннику, для позначення століть, для нумерації розділів книжки тощо.

Римські цифри відповідають таким числам:

Натуральні числа римськими цифрами записують за допомогою повторення цифр. При цьому якщо менша цифра стоїть після більшої, то маємо суму відповідних цифр, а якщо менша цифра стоїть перед більшою, то маємо різницю відповідних цифр. Наприклад, \(XVIII = 10 + 5 + 1 + 1 + 1 = 18, LX = 50 + 10 = 60, IV = 5 - 1 = 4, XC = 100 - 10 = 90\).

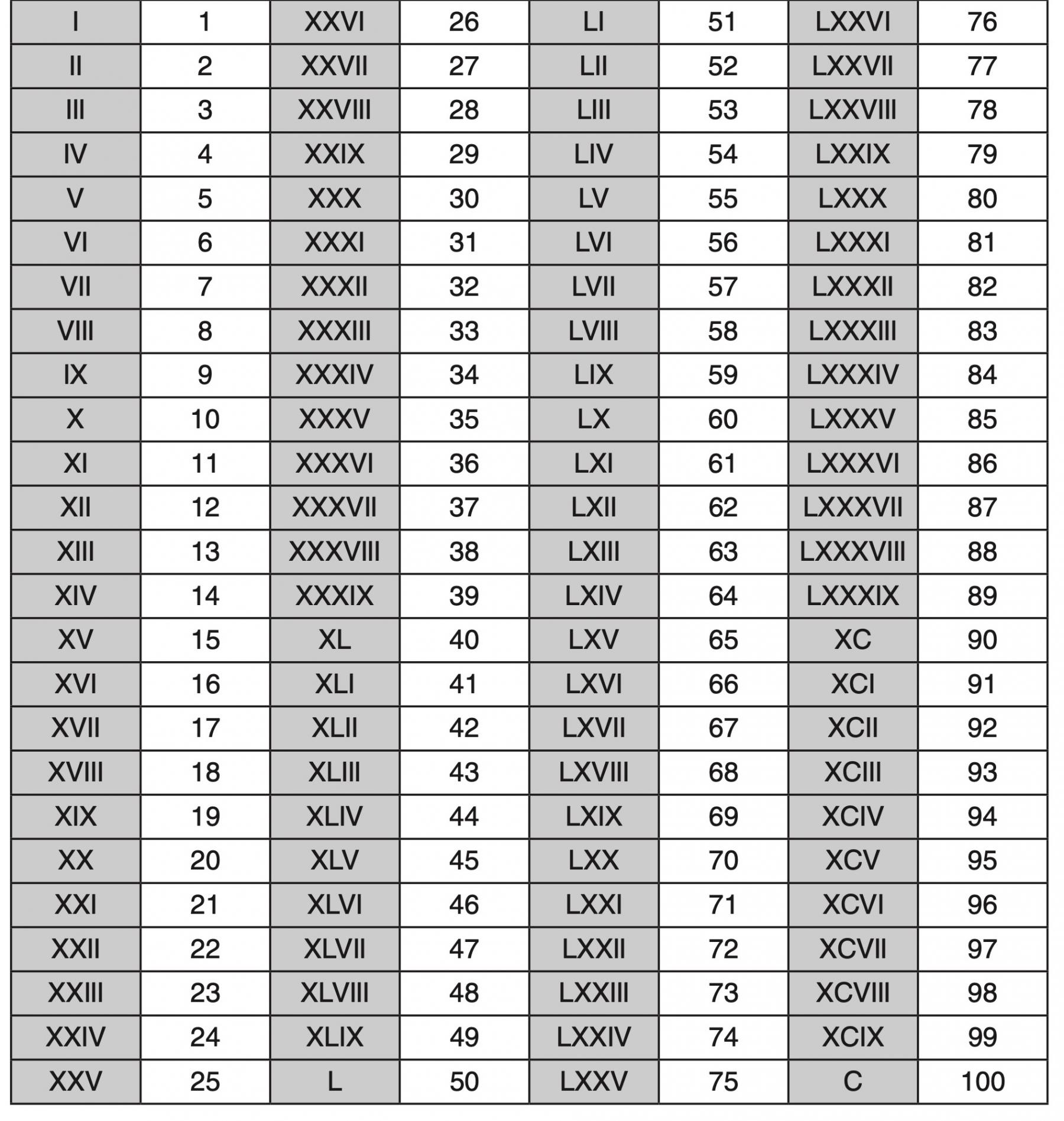
Також зручно користуватися таблицею для переведення римських чисел в арабські та навпаки арабські в римські числа