Квадратичная функция
Определение
Функцию, которую можно задать формулой вида \(y=ax^{2}+bx+c\), где \(x\)- независимая переменная, \(a, b, c\) — некоторые числа, причем \(a \neq0\), называют квадратичной.
Общее представление о графике квадратичной функции дают координаты вершины параболы и направление ее ветвей. Это представление будет тем полнее, чем больше точек, принадлежащих графику, мы узнаем. Поэтому можно строить график квадратичной функции, не используя параллельных переносов по следующей схеме:
\(1\)) найти абсциссу вершины параболы по формуле \(x_{0}=-\frac{b}{2a}\);
\(2\)) найти ординату вершины параболы по формуле
\(y_{0}=\frac{4ac-b^{2}}{4a}=-\frac{D}{4a}\),
где \(D\) - дискриминант квадратного трехчлена \(ax^{2}+bx+c\);
Формулу \(y_{0}=\frac{4ac-b^{2}}{4a}=-\frac{D}{4a}\) запоминать необязательно. Достаточно вычислить значение функции \(y=ax^{2}+bx+c\) в точке с абсциссой \(x_{0}=-\frac{b}{2a}\)
\(3\)) определить направление ветвей параболы;
Коэффициент \(a\) квадратного трехчлена \(ax^{2}+bx+c\) определяет направление ветвей параболы: при \(а>0\) ветки направлены вверх, при \(a<0\) — вниз.
\(4\)) найти координаты еще нескольких точек, принадлежащих искомому графику, в частности координаты точек пересечения параболы с осью абсцисс (если данная функция имеет нули).
С осью \(Ox\): \(y=0\), то \(ax^2+bx+c=0\), решаем квадратное уравнение и находим еще две точки графика;
С осью \(Oy\): \(x=0\), то \(y=c\).
\((0;c)\) — координаты точки пересечения параболы с осью ординат;
обозначить эти точки на координатной плоскости;
\(5\)) провести через все обозначенные точки плавную непрерывную линию.
Рассмотрим пример
Постройте график функции \(y=-x^2+2x+3\)
Решение:
Найдем абсциссу вершины параболы, поскольку \(a=-1, b=2, c=3\), то \(x_{0}=-\frac{2}{2\cdot(-1)}=1\).
Найдем ордината вершины параболы \(y_{0}=-1\cdot1^2+2\cdot1+3=4\).
\((1;4)\) — вершина параболы.
Ветки направлены вниз, поскольку \(a=-1\), то есть \(a<0\).
Найдем пересечение графика с осью Ox: поскольку y=0, то получим уравнение \(-x^2+2x+3=0\), как решать квадратные уравнения читайте здесь. Следовательно x1=-1, \(x_{2}=3\). Получили точки \((-1;0)\) и \((3;0)\).
Найдем пересечение графика с осью \(Oy\): поскольку \(x=0\), то \(y=-1\cdot0^2+2\cdot0+3=3\). Получили точку \((0;3)\).
Провести через все обозначенные точки плавную непрерывную линию.
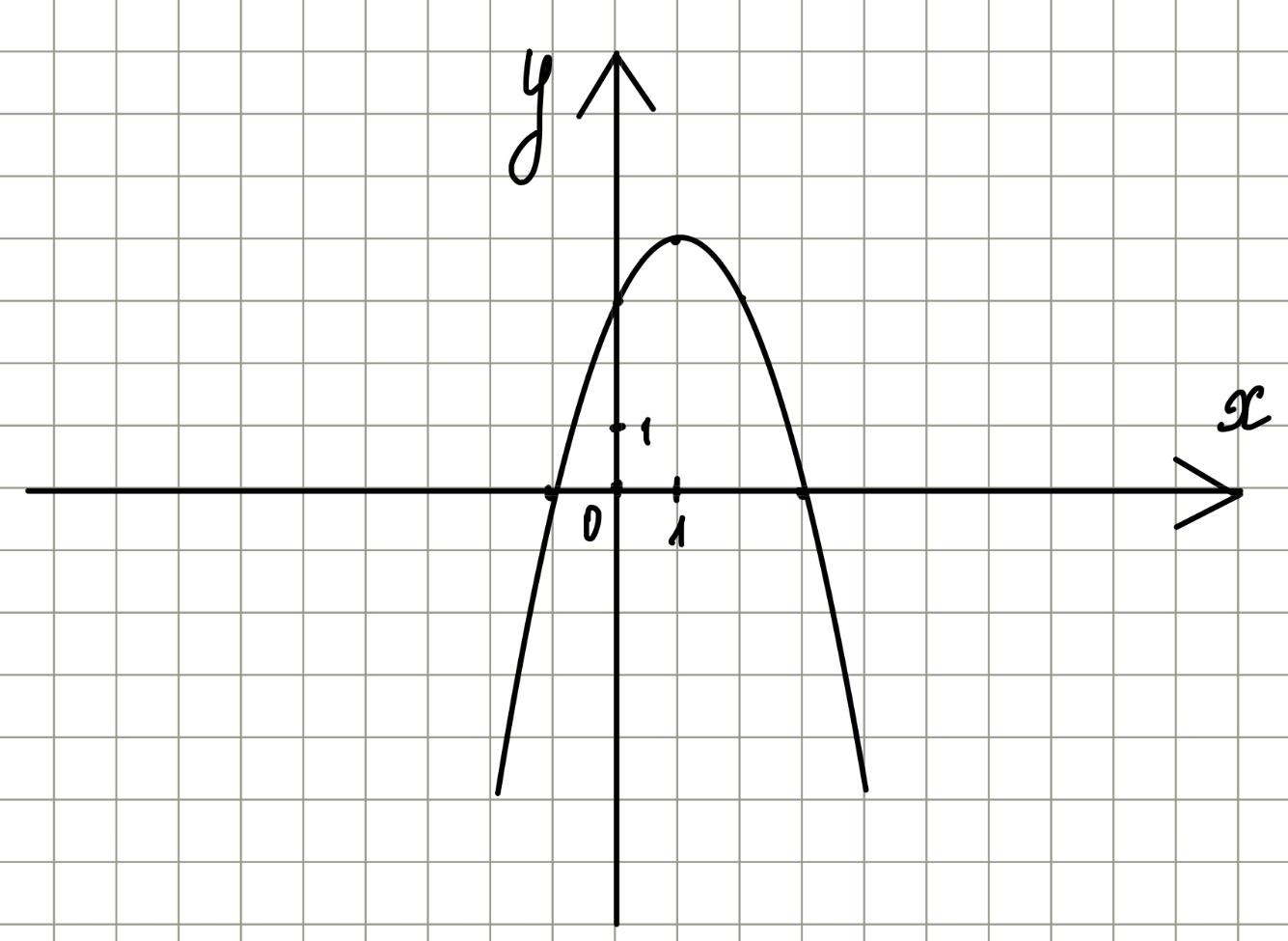
Если внимательно посмотреть на грифик, можно заметить ось симметрии \(x=1\).
