Теорема Пифагора
Теорема Пифагора — одна из основных теорем евклидовой геометрии. Она устанавливает отношения между сторонами в прямоугольном треугольнике.
Теорема (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
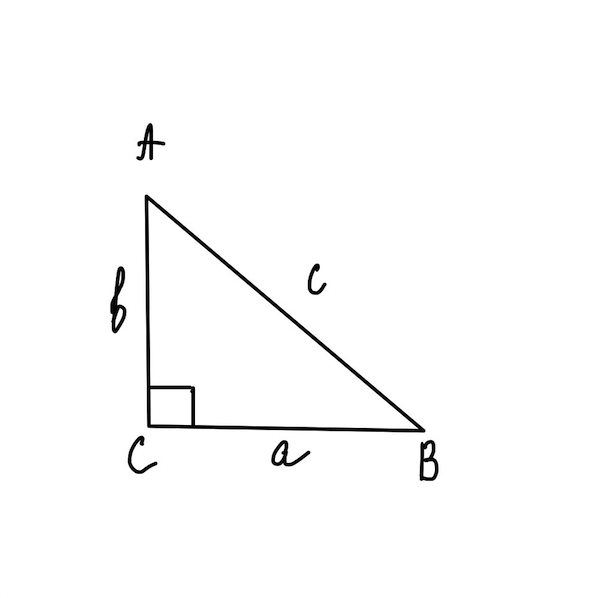
Если в прямоугольном треугольнике длины катетов равны \(a\) и \(b\), а длина гипотенузы равна \(c\), то теорему Пифагора можно выразить следующим равенством:
\(c^ 2 =a^ 2+ b^ 2\)
Теорема Пифагора позволяет по двум сторонам прямоугольного треугольника найти его третью сторону:
\(c=\sqrt{a^{2}+b^{2}}\);
\(a=\sqrt{c^{2}-b^{2}}\);
\(b=\sqrt{c^{2}-a^{2}}\).
Теорема Пифагора — это частный случай теоремы косинусов. Это объясняется тем, что косинус \(90^{\circ}\) равен нулю, поэтому удвоенное произведение исчезает.
Теорема Фалеса. Теорема о пропорциональных отрезках
Теорема Фалеса — это свойство параллельных прямых, пересекающих две прямые с общей точкой.
Теорема (теорема Фалеса). Если параллельные прямые, пересекающие стороны угла, отсекают на одной стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
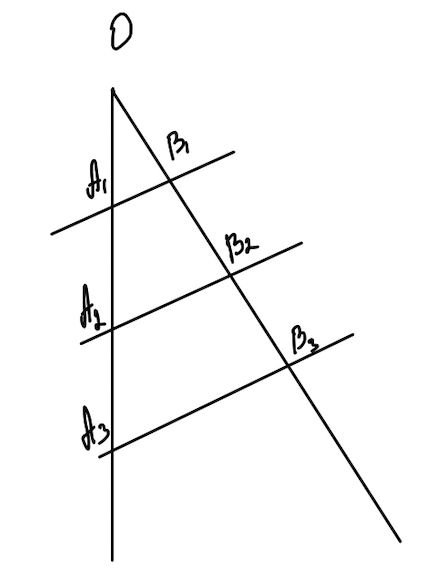
Если \(A_{1}A_{2}=A_{2}A_{3}\), то \(B_{1}B_{2}=B_{2}B_{3}\).
Обобщена теорема Фалеса. Параллельные прямые, пересекающие две заданные прямые \(а\) и \(b\), отсекают на них пропорциональные отрезки.
Теорема косинусов
Теорему Пифагора легко запомнить, она часто используется в прямоугольных треугольниках. На самом деле, теорема Пифагора работает для любого треугольника, только называется она теорема косинусов.
Теорема (теорема косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
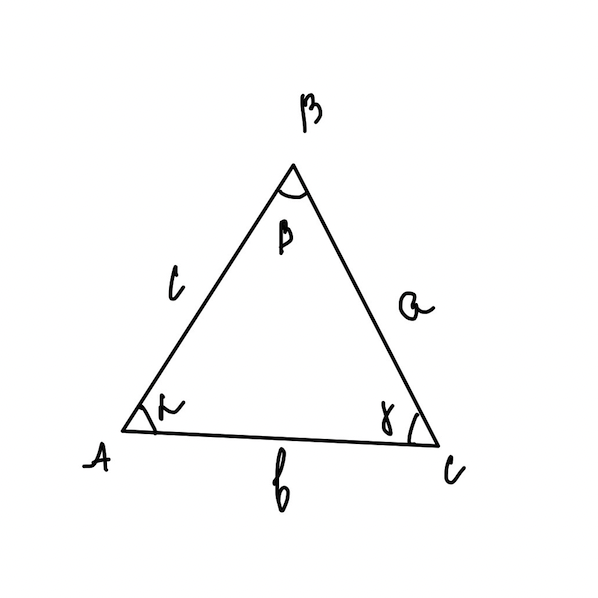
\(a^{2}=b^{2}+c^{2}-bc \cos\alpha\)
Из формулы сразу понятно, почему она называется теоремой косинусов. Она очень похожа на квадрат разницы с учетом косинуса, потому ее запомнить не сложно. Если упомянуть что косинус \(90^{\circ}\) это 0, то мы увидим уже знакомую теорему Пифагора. Мы уже подробно изучали теорему косинусов и рассматривали примеры.
Теорема синусов
Теорема синусов — это формула отношения стороны к синусу противоположного угла в треугольнике.
Теорема (теорема синусов). Стороны треугольника пропорциональны синусам противоположных углов.
\(\frac{a}{ sin\alpha}=\frac{b}{ sin\beta}=\frac{c}{ sin\gamma}=2R\)
По теориме синусов можно найти радиус описанной окружности по известной стороне и противоположному углу или неизвестную сторону или угол. На ДПА или ВНО теорема синусов встречается не часто, но знать ее нужно.
Теорема Менелая
Ее также называют теоремой о треугольнике и прямой, и звучит она так:
Теорема (теорема Менелая) На сторонах \(AB\) и \(BC\) треугольника ABC обозначены соответственно точки \(C_{1}\) и \(A_{1}\) , а на продолжении стороны \(AС\) - точку \(B_{1}\). Для того чтобы точки \(A_{1}, B_{1}, C_{1}\) лежали на одной прямой, необходимо и достаточно, чтобы выполнялось равенство:
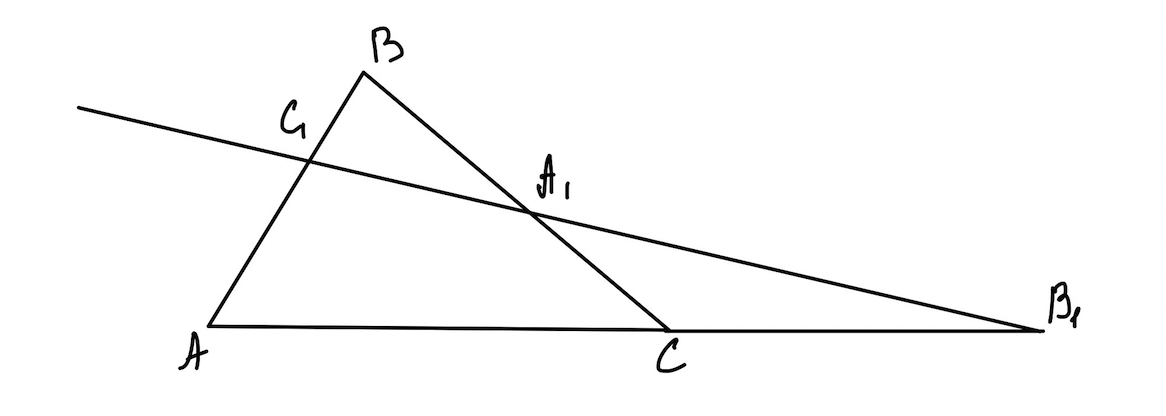
\(\frac{AC_{1}}{C_{1}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}=1\)
