Свойство биссектрисы треугольника
Сегодня разберем тему по геометрии 8 класса: «Свойство биссектрисы треугольника».
Важно для усвоения данной темы:
— понять формулировку теоремы;
— владеть пропорциями (6 класс);
— правильно составить пропорцию.
Выполнив условие выше, правильно решена задача по геометрии у тебя в тетради!
Также доступны видео по теме «Свойство биссектрисы треугольника» на YouTube канале Tutor-Math в двух частях.
Разбор темы вместе с репетитором математики.
Начнём с определения. Вспомним, что такое треугольник.
Определение. Треугольником называют геометрическую фигуру, состоящую из трех точек, не лежащих на одной прямой, и трех соединяющих их отрезков.
И что такое биссектриса.
Определение. Отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину с точкой противоположной стороны, называют биссектрисой.
Перейдем к формулировке теоремы.
Теорема. Биссектриса треугольника делит сторону, к которой она проведена, на отрезки, пропорциональные двум другим сторонам.
Рассмотрим типовые задачи из учебника Истер 8 класс.
№\(563\). \(ВР\) — биссектриса треугольника \(АВС\) (рис. 1). \(АР : PC = 1 : 2\), \(AB = 4\) см. Найдите \(BC\).
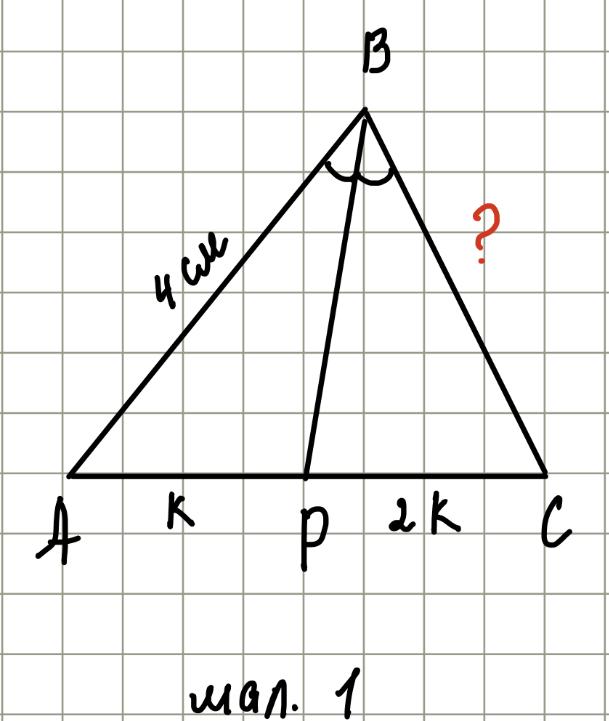
Дано: \( \triangle ABC\), \(ВР\) — биссектриса, \(АР : PC = 1 : 2\), \(AB = 4\) см.
Найти: \(BC\).
Решение: по свойству биссектрисы \(AB : BC=AP : PC\), поскольку \(АР : PC = 1 : 2\), то \(AB : BC = 1 : 2\). Подставим \(AB = 4\) см в найденное отношение, получим \(4 : BC = 1 : 2\), отсюда \(BC = 8\) см.
Ответ: \(8\) см.
№\(570\). Биссектриса треугольника делит сторону на отрезки, разница длин которых \(1\) см. Найдите периметр треугольника, если две другие стороны равны \(8\) см и \(6\) см.
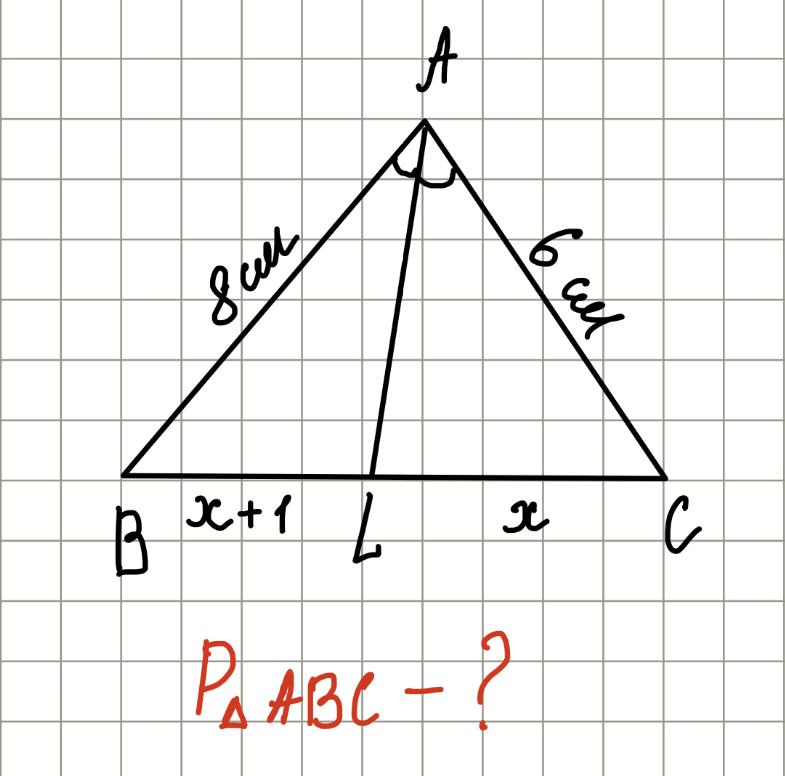
Дано:\( \triangle ABC\), \(AL\) — биссектриса, \(AB=8см\), \(AC=6\)см, \(BL-LC=1\) см.
Найти: \(P_^{\triangle ABC^}\).
Решение: по свойству биссектрисы треугольника \(AB:AC=BL:LC\). Пусть \(LC=x\), тогда \(BL=1+x\). Подставляем в пропорцию известные величины \(8:6=x+1:x\).
Важно, что большая сторона относится к большей, меньшей к меньшей.
По свойству пропорции получим уравнение:
\(8x=6x+6\);
\(8x-6x=6\);
\(2x=6\);
\(x=3 см\).
\(LC=3см\), \(BL=4 см\), вся сторона \(BC=3+4=7\) см. Периметр треугольника: \(P_^{\triangle ABC^} = AB+BC+AC= 8+7+6=21\) см.
Ответ: \(21\) см.
№\(573\). В треугольнике, стороны которого равны \(15\) см, \(21\) см и \(24\) см, проведен полукруг, центр которого принадлежит большей стороне треугольника и касающийся двух других сторон. На какие отрезки центр полукруга делит большую сторону?
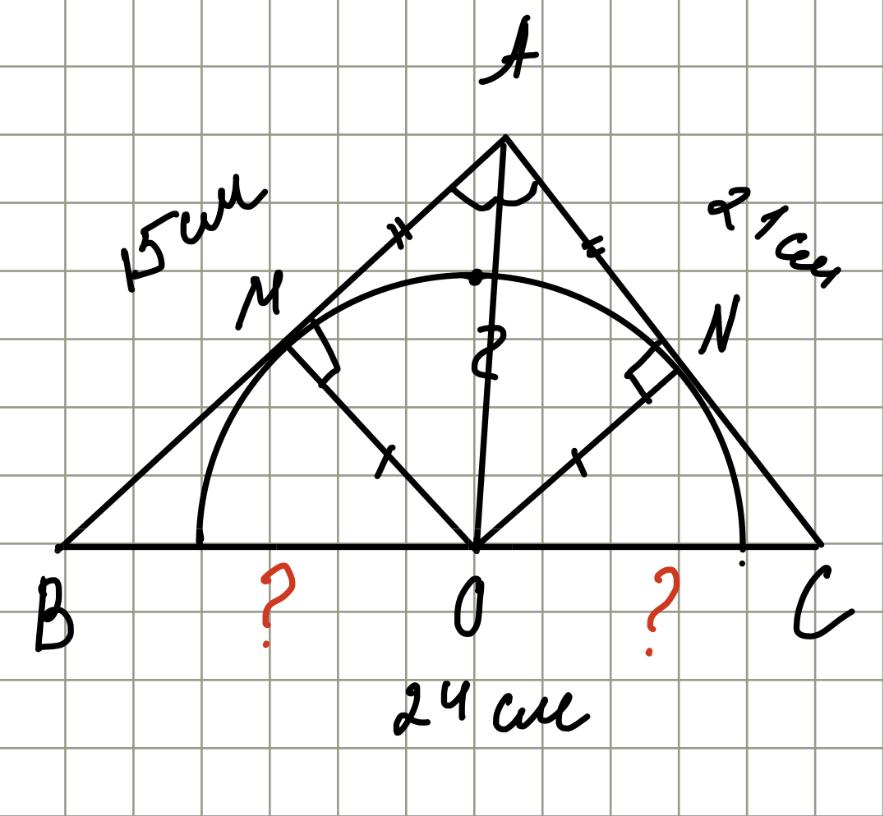
Дано: \(\triangle ABC\) треугольник, \(AB=15\) см, \(AC=21\) см, \(BC=24\) см, круг с центром в т.\(O\), \(M\) и \(N\) - точки соприкосновения.
Найти: \(BO\), \(CO\).
Решение: проведем отрезки \(MO\), \(AO\), \(NO\). \(OM\bot AB\), \(ON\bot AC\) как радиусы произведены в точки соприкосновения. \(AO\) - общая сторона для треугольников \(\triangle OMA\) \(\triangle ONA\), \(OM = ON\) как радиусы, \(AM = AN\) по свойству отрезков соприкасающихся. Тогда \(\triangle OMA = \triangle ONA\). По трем сторонам: \(\triangle MAO = \triangle NAO\), \(AO\) - биссектриса \(\triangle ABC\). По свойству биссектрисы треугольника \(AB : AC = BO : CO\) подставим известные значения и сократим на \(3\) \(BO : CO = 5 : 7\). Пусть \(x\) — коэффициент пропорциональности, тогда \(BO = 5x\), \(CO = 7x\). Составляем уравнение:
\(5x+7x=24\);
\(12x=24\);
\(x=24:12\);
\(x=2\).
\(BO = 5x = 5\cdot2 = 10\)см,
\(CO = 7x = 7\cdot2 = 14\)см.
Ответ: \(10\)см, \(14\)см.
Читайте статью репетитора по математике: «Топ 5 теорем по геометрии для ДПА и ЗНО».
