Теорема косинусів
9 клас – насичений новими знаннями час. Щоб не заплутатися в теорії з геометрії, рекомендуємо записатися на уроки в Tutor-Math. У цій статті ви знайдете найважливіше про теорему косинусів.
Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін і косинуса кута між ними.
\[a^{2}=b^{2}+c^{2}-bc \cos\alpha\]
Зауважимо, що теорема Піфагора є окремим випадком теореми косинусів для прямокутного трикутника, тому її інколи називають узагальненою теоремою Піфагора.
Отже, у довільному трикутнику \(АВС\) виконуються рівності:
\(c^ 2 =a^ 2+ b^ 2-2abcosC\);
\(b^ 2 =a^ 2+ c^ 2-2accosB\);
\(a^ 2 =b^ 2+ c^ 2-2bccosA\).
Порада: щоб швидше розібратися у складній темі, запишіться на онлайн заняття з математики для дітей та підлітків.
За допомогою теореми косинусів можна, наприклад, знайти невідому сторону трикутника, якщо відомо дві його інші сторони й один з кутів.
Наприклад косинус кута \(С\) можна знайти за формулою, виразивши \(cosС\) з формули теореми косинусів:
\(cosC=\frac{a^ 2+ b^ 2-c^ 2}{2ab}\).
Отже, теорема косинусів допомагає розв'язувати трикутники.
Теорема косинусів є зручною і для визначення виду трикутника. Щоб установити гострокутним, прямокутним або тупокутним є трикутник досить знайти знак косинуса його найбільшого кута. З формули косинуса кута зрозумло, що знак косинуса кута залежить від знака чисельника дробу, оскільки знаменник завжди додатний. Тому знак виразу \(a^ 2+ b^ 2-c^ 2\) дозволяє визначити знак косинуса кута трикутника, а отже, і вид цього кута (гострий, прямий чи тупий).
Якщо \(c\) - найбільша сторона трикутника і
\(a^ 2+ b^ 2-c^ 2>0\), то кут \(C\) - гострий, а трикутник - гострокутний;
\(a^ 2+ b^ 2-c^ 2=0\), то кут \(C\) - прямий, а трикутник - прямокутний;
\(a^ 2+ b^ 2-c^ 2< 0\), то кут \(C\) - тупий, а трикутник - тупокутний.
Також, за допомогою теореми косинусів можна довести формулу медіани трикутника:
\(m_{a}= \frac{1}{2}\sqrt{2b^ 2+ 2c^ 2-a^ 2}\).
Розв`яжемо декілька типових задач з цієї теми.
Задача 1. Знайдіть невідому сторону трикутника \(АВС\), якщо \(AB=5\) см, \(BC=8\) см, \( \angle B= 60^{\circ}\).
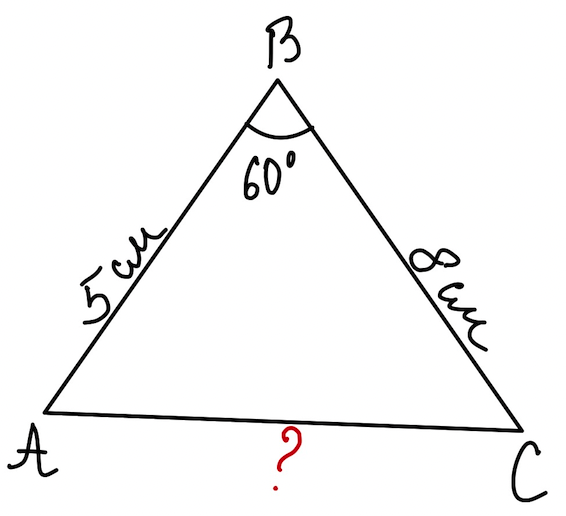
Дано: \(\triangle ABC\) , \(AB=5\) см, \(BC=8\) см, \( \angle B= 60^{\circ}\).
Знайти: \(AC \).
Розв`язання:
За теоремою косинусів:
\(AC^ 2=AB^ 2+BC^ 2-2\cdot AB\cdot BC\cdot cosB\).
Підставляємо дані з умови в формулу і отримуємо:
\(AC^ 2=5^ 2+8^ 2-2\cdot 5\cdot 8\cdot cos 60^{\circ}=25+64-2\cdot 5\cdot 8\cdot \frac{1}{2}=49\),
\(AC=7\) см.
Відповідь: \(AC=7\) см.
Задача 2. Доведіть, що трикутник зі сторонами \(8\) см, \(15\) см і \(17\) см є прямокутним.
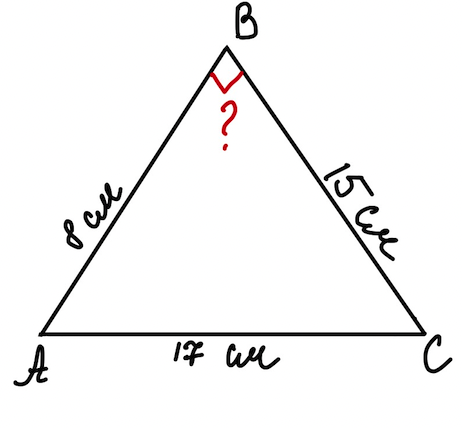
Дано: \(\triangle ABC\), \(AB=8\) см, \(BC=15\) см і \(AC=17\) см.
Довести: \(\triangle ABC\) - прямокутний.
Доведення:
\(AC\) - найбільша сторона \(\triangle ABC\). Порівняємо з \(0\) значення виразу \(AB^ 2+BC^ 2-AC^ 2\). Підставляємо дані з умови \(8^ 2+15^ 2-17^ 2=64+225-289=0\), отже \( \angle A\) - прямий, а \(\triangle ABC\) - прямокутний.
Задача 3. Дві сторони трикутника дорівнюють \(7\) см і \(8\) см, а кут проти меншої з них \(60^{\circ}\). Знайдіть третю сторону трикутника.
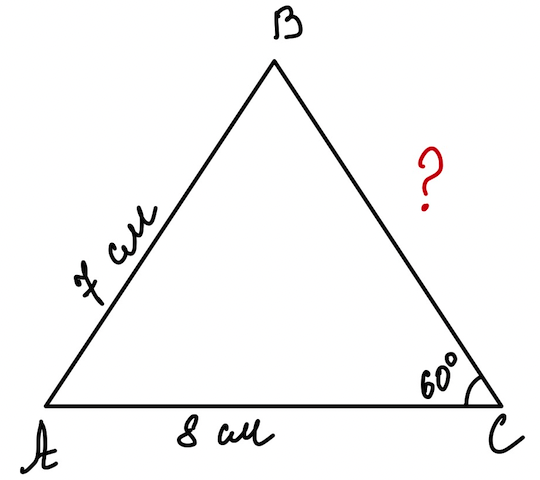
Дано: \(\triangle ABC\), \(AB=7\) см, \(AC=8\) см, \( \angle C=60^{\circ}\).
Знайти: \(BC\).
Розв`язання:
Нехай, сторона \(\triangle ABC\) \(BC=x\), тоді за теоремою косинусів маємо: \(AB^ 2=BC^ 2+AC^ 2-2\cdot BC\cdot AC\cdot cosC\).
Підставимо значення з умови задачі, отримаємо \(7^ 2=x^ 2+8^ 2-2\cdot 8\cdot x\cdot \frac{1}{2}\);
\(49=x^ 2+64-8x\);
\(x^ 2-8x+15=0\)
Розв`язуємо квадратне рівняння. Як розв`язувати квадратні рівняння описано в цій статті.
\(D=64-60\), \(\sqrt{D}=2\)
\(x_1=5, x_2=3\)
\(BC=5\) см, або \(3\) см.
Відповідь: \(3\) см або \(5\) см.
Задача 4. У рівнобедреному трикутнику основа дорівнює \(8\) см, а кут при основі - \(45^{\circ}\). Знайдіть бічну сторону трикутника.
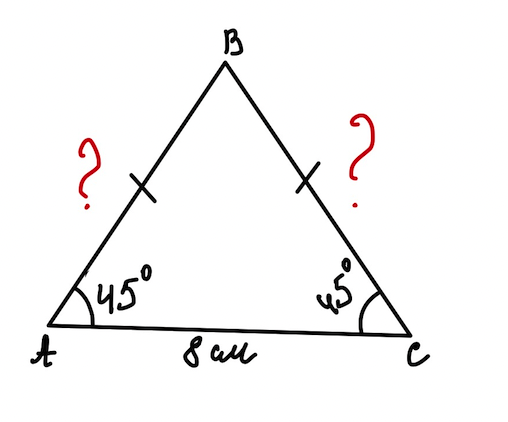
Дано: \(\triangle ABC\), \(AB=BC\), \(AC=8\) см, \( \angle A=45^{\circ}\).
Знайти: \(AB\).
Розв`язання:
Оскільки \(\triangle ABC\) - рівнобедрений, \(AB=BC\), \( \angle A= \angle C=45^{\circ}\). Знайдемо \( \angle B\). За теоремою про суму кітів в трикутнику \( \angle B=180^{\circ}-\angle A- \angle C=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}\). Нехай \(AB=BC=x\).
За теоремою косинусів:
\(AC^ 2=AB^ 2+BC^ 2-2\cdot AB\cdot BC\cdot cosB\);
\(64=x^ 2+x^ 2\);
\(2x^ 2=64\);
\(x^ 2=32\);
\(x=4\sqrt{2}\).
\(AB=BC=4\sqrt{2}\) см.
Відповідь: \(4\sqrt{2}\) см.
Задача 5. Знайдіть косинус найбільшого кута трикутника, сторони якого дорівнюють \(5\) см, \(6\) см і \(9\) см.
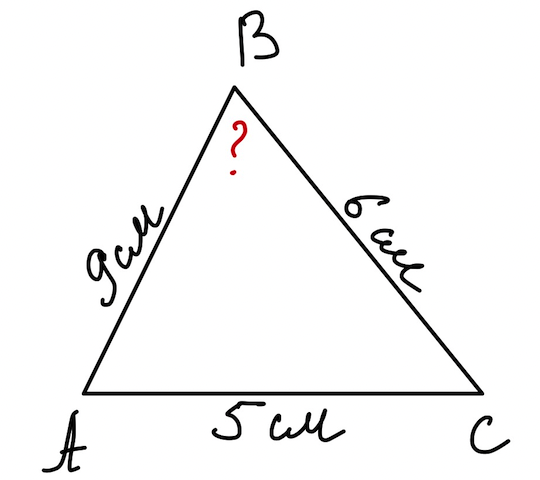
Дано: \(AB=9\) см, \(BC=6\) см, \(AC=5\) см.
Знайти: \(cos\angle B\).
Розв`язання:
Найбільший кут лежить навпроти найбільшої сторони. За теоремою косинусів: \(cos\angle B=\frac{BC^ 2+ AC^ 2-AB^ 2}{2BC\cdot AC}=\frac{6^ 2+ 5^ 2-9^ 2}{2\cdot 6\cdot 5}=\frac{-20}{12\cdot 5}=-\frac{1}{3}\).
Відповідь: \(cos\angle B=-\frac{1}{3}\).
Залишилися запитання? Чекаємо на наших уроках і ми з радістю дамо відповіді на всі запитання з обраного предмету.
