Властивість бісектриси трикутника
Сьогодні розберемо тему з геометрії 8 класу: "Властивість бісектриси трикутника".
Важливо для засвоєння даної теми:
— зрозуміти формулювання теореми;
— володіти пропорціями ( 6 клас);
— правильно скласти пропорцію.
Виконавши умови вище, правильно розвʼязана задача з геометрії в тебе в зошиті!
Також доступні відео з теми «Властивість бісектриси трикутника» на YouTube каналі Tutor-Math у двох частинах.
Розбір теми разом з репетитором математики.
Почнемо з означення. Пригадаємо, що таке трикутник.
Означення. Трикутником називають геометричну фігуру, що складається з трьох точок, які не лежать на одній прямій, і трьох відрізків, які сполучають їх.
Та що таке бісектриса.
Означення. Відрізок, що є частиною бісектриси кута трикутника і сполучає вершину з точкою протилежної сторони, називають бісектрисою.
Перейдемо до формулювання теореми.
Теорема. Бісектриса трикутника ділить сторону, до якої вона проведена, на відрізки, пропорційні двом іншим сторонам.
Розглянемо типові задачі з підручника Істер 8 клас.
№ \(563\). \(ВР\) — бісектриса трикутника \(АВС\) (мал. 1). \(АР : PC = 1 : 2\), \(AB = 4\) см. Знайдіть \(BC\).
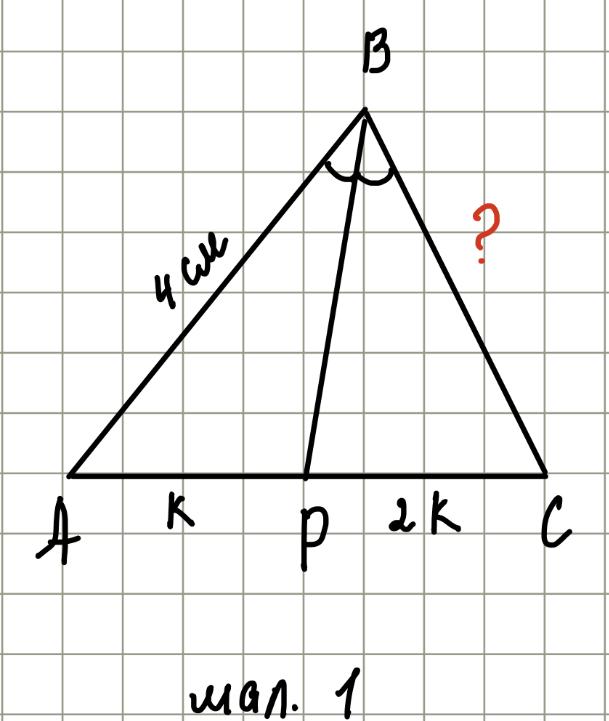
Дано: \( \triangle ABC\), \(ВР\) — бісектриса, \(АР : PC = 1 : 2\), \(AB = 4\) см.
Знайти: \(BC\).
Розвʼязання: за властивістю бісектриси \(AB : BC=AP : PC\), оскільки \(АР : PC = 1 : 2\), то \(AB : BC = 1 : 2\). Підставимо \(AB = 4\) см в знайдене відношення, отримаємо \(4 : BC = 1 : 2\), звідси \(BC = 8\) см.
Відповідь: \(8\) см.
№ \(570\). Бісектриса трикутника ділить сторону на відрізки, різниця довжин яких \(1\) см. Знайдіть периметр трикутника, якщо дві інші сторони дорівнюють \(8\) см і \(6\) см.
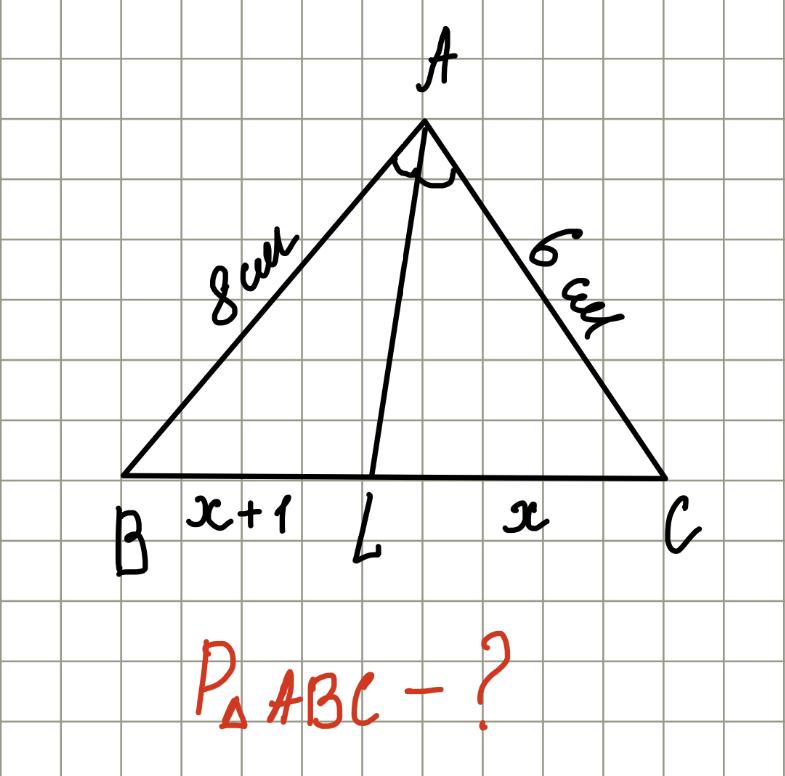
Дано:\( \triangle ABC\), \(AL\) — бісектриса, \(AB=8см\), \(AC=6\)см, \(BL-LC=1\) см.
Знайти: \(P_{\triangle ABC}\).
Розвʼязання: за властивістю бісектриси трикутника \(AB : AC=BL : LC\). Нехай \(LC=x\), тоді \(BL=1+x\). Підставляємо в пропорцію відомі величини \(8:6=x+1:x\).
Важливо, що більша сторона відноситься до більшої, менша до меншої.
За властивістю пропорції отримаємо рівняння:
\(8x=6x+6\);
\(8x-6x=6\);
\(2x=6\);
\(x=3 см\).
\(LC=3см\), \(BL=4 см\), вся сторона \(BC=3+4=7\) см. Периметр трикутника: \(P_{\triangle ABC} = AB+BC+AC=8+7+6=21\) см.
Відповідь: \(21\) см.
№ \(573\). У трикутнику, сторони якого дорівнюють \(15\) см, \(21\) см і \(24\) см, проведено півколо, центр якого належить більшій стороні трикутника і яке дотикається до двох інших сторін. На які відрізки центр півкола ділить більшу сторону?
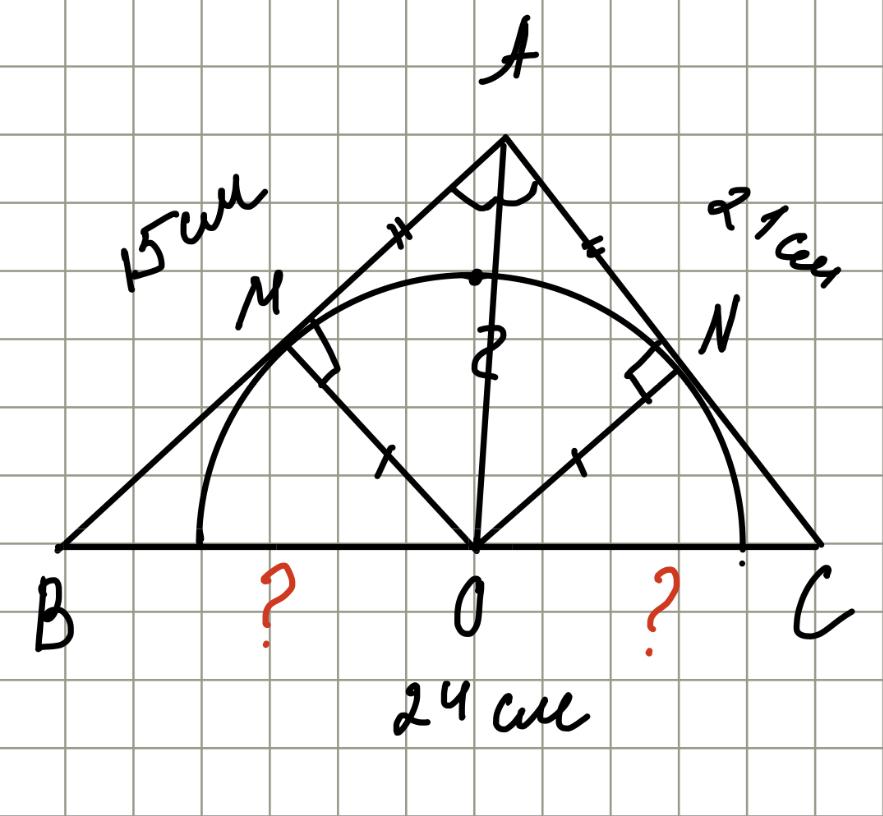
Дано: \(\triangle ABC\) трикутник, \(AB=15\) см, \(AC=21\) см, \(BC=24\) см, коло з центром в т.\(O\), \(M\) і \(N\) - точки дотику.
Знайти: \(BO\), \(CO\).
Розвʼязання: проведемо відрізки \(MO\), \(AO\), \(NO\). \(OM\bot AB\), \(ON\bot AC\) як радіуси проведені в точки дотику. \(AO\) - спільна сторона для трикутників \(\triangle OMA\) \(\triangle ONA\), \(OM = ON\) як радіуси, \(AM = AN\) за властивістю відрізків дотичних. Тоді \(\triangle OMA = \triangle ONA\). За трьома сторонами: \(\triangle MAO = \triangle NAO\), \(AO\) - бісектриса \(\triangle ABC\). За властивістю бісектриси трикутника \(AB : AC = BO : CO\) підставимо відомі значення і скоротимо на \(3\) \(BO : CO = 5 : 7\). Нехай \(x\) - коефіцієнт пропорційності, тоді \(BO = 5x\), \(CO = 7x\). Складаємо рівняння:
\(5x+7x=24\);
\(12x=24\);
\(x=24:12\);
\(x=2\).
\(BO = 5x = 5\cdot2 = 10\)см,
\(CO = 7x = 7\cdot2 = 14\)см.
Відповідь: \(10\)см, \(14\)см.
Читайте статтю репетитора з математики: "Топ 5 теорем з геометрії для ДПА та ЗНО".
